



Next: The Next Bit Theorem
Up: Pseudo-random number generators
Previous: Pseudo-random number generators
Contents
The Quadratic Generator
Let 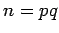 , where
, where 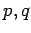 are primes
are primes
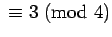 . For each prime,
. For each prime,  is a square if and only if
is a square if and only if 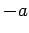 is not
a square (Lemma 22).
This implies that, if
is not
a square (Lemma 22).
This implies that, if
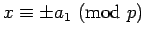 and
and
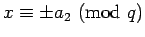 ,
there will be exactly one choice which makes
,
there will be exactly one choice which makes 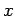 a square mod
a square mod 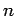 .
Hence, if
.
Hence, if 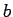 is a square mod
is a square mod 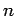 , exactly one of its four square roots
will also be a square. This principal square root will be
denoted by
, exactly one of its four square roots
will also be a square. This principal square root will be
denoted by 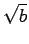 .
.
The quadratic generator uses a randomly chosen square 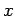 (called the
seed) not divisible by
(called the
seed) not divisible by  or
or 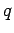 to generate a sequence of
0's and 1's (bits). The sequence is
to generate a sequence of
0's and 1's (bits). The sequence is 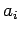 mod 2, where
mod 2, where 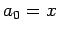 and
and
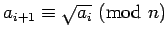 :
:
(from a practical point of view, it is simpler to generate the sequence
starting with the last number and squaring)
As a small example with 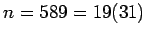 and
and 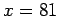 , the sequence of
, the sequence of 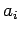 is
is
(note
that 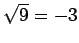 , not 3) which gives the sequence of bits 11010101.
, not 3) which gives the sequence of bits 11010101.
Translated from LaTeX by Scott Sutherland
2002-12-14
![]() (called the
seed) not divisible by
(called the
seed) not divisible by ![]() or
or ![]() to generate a sequence of
0's and 1's (bits). The sequence is
to generate a sequence of
0's and 1's (bits). The sequence is ![]() mod 2, where
mod 2, where ![]() and
and
![]() :
:
![]() and
and ![]() , the sequence of
, the sequence of ![]() is
is