



Next: The Greatest Common Divisor
Up: Introduction to Number Theory
Previous: Introduction to Number Theory
Contents
The congruence
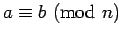 (``
(`` is congruent to
is congruent to 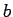 mod
mod 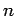 '') says that,
when divided by
'') says that,
when divided by 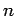 ,
,  and
and 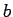 have the same remainder.
have the same remainder.
In the second congruence, we are using 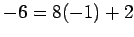 . We always have
. We always have
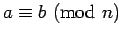 for some
for some 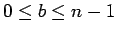 , and we are usually concerned with
that
, and we are usually concerned with
that 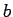 . If
. If
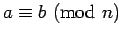 and
and 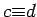 , we can add or multiply
, we can add or multiply
Division does not always work:
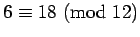 , but
, but
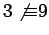 .
.
Translated from LaTeX by Scott Sutherland
2002-12-14