


Next: The Efficient Test Theorem
Up: Pseudo-random number generators
Previous: The Quadratic Generator
It would certainly be undesirable if there were an efficient algorithm
which took as input the first 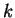 bits of the sequence from the generator
and guessed the
bits of the sequence from the generator
and guessed the 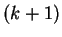 -st bit with probability much greater than
-st bit with probability much greater than 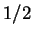 .
We say a generator satisfies the Next Bit Condition if there is
no such algorithm.
.
We say a generator satisfies the Next Bit Condition if there is
no such algorithm.
Theorem 29
If (QRA) is true, the quadratic generator
satisfies the Next Bit Condition.
Proof: We will show that
an algorithm that could predict the 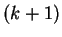 -st bit could be used to
distinguish squares from pseudo-squares mod
-st bit could be used to
distinguish squares from pseudo-squares mod 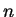 .
.
Let
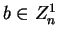 .
The
sequence of length
.
The
sequence of length 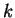
can be considered as coming from the quadratic generator with seed the
first term of the sequence. If we take this sequence mod 2 and give
it to our predictor, we would get a guess as to whether
which has probability 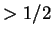 of being
right. The principle square root of
of being
right. The principle square root of 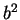 is
is 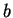 if
if 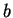 is a square,
is a square,
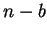 if
if 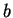 is a pseudo-square. Since
is a pseudo-square. Since
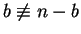 mod 2, the
information from the predictor gives us a guess as to whether
mod 2, the
information from the predictor gives us a guess as to whether 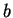 is
a square.
is
a square.



Next: The Efficient Test Theorem
Up: Pseudo-random number generators
Previous: The Quadratic Generator
Translated from LaTeX by Scott Sutherland
1998-03-15
![]() .
The
sequence of length
.
The
sequence of length ![]()