Defining relations for reflections. I
oleg.viro@gmail.com
Abstract.
An idea to present a classical Lie group of positive dimension by generators and relations sounds dubious, but happens to be fruitful. The isometry groups of classical geometries admit elegant and useful presentations by generators and relations. They are closely related to geometry and allow to make fast and efficient calculations in the groups. In this paper simple presentations of the isometry groups of Euclidean plane, 2-sphere, the real projective plane and groups $SO(3)$ and $O(n)$ are introduced.
1. Isometries of the Euclidean plane
1.1. Well-known facts
See, e.g., [2].
Classification. Any isometry of the Euclidean plane is either the identity $\operatorname{id}$, or a reflection in a line, or a translation, or a rotation about a point, or a glide reflection (composition of a reflection in a line and a translation along the same line).
Generators. Any isometry is a composition of at most three reflections in lines.
Compositions of refections. The composition $R_{m}\circ R_{l}$ of reflections $R_{l}$ and $R_{m}$ in lines $l$ and $m$, respectively, is
-
the identity if $l=m$;
-
a translation if $l\parallel m$;
-
a rotation if $l$ is transverse to $m$.
If $l\parallel m$, then the translation $R_{m}\circ R_{l}$ moves any point by a distance twice greater than the distance between the lines in the direction perpendicular to these lines.
If $l$ is transverse to $m$, then the composition $R_{m}\circ R_{l}$ is a
rotation about the intersection point $m\cap l$ by the angle twice greater
than the angle between the lines. See figure
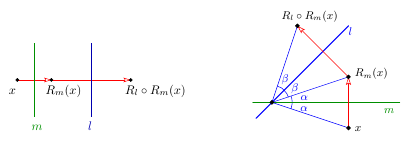
Obviously, in this way any translation and any rotation can be presented as a composition of two reflections.
1.2. Relations among reflections
Presentations of a translation or a rotation as a composition of two reflections are not unique.
Any pair of lines perpendicular to the direction of a translation and having the same distance from each other gives a presentation of the same translation.
Any pair of lines meeting at the center of the rotation and forming the same angle gives a presentation of the same rotation.
This non-uniqueness of presentations can be formulated as relations among reflections in lines. Each such relation involves four reflections and has form
| $R_{m}\circ R_{l}=R_{m^{\prime}}\circ R_{l^{\prime}}.$ | (1) |
The lines $l$, $m$, $l^{\prime}$ and $m^{\prime}$ belong to the same pencil: either all four lines are parallel, or all four pass through the same point.
The pencils of lines have natural metrics: in a pencil of parallel lines this is the usual distance between parallel lines; in a pencil of lines having a common point this is the usual angle between lines. In either case, for the lines $l$, $m$, $l^{\prime}$ and $m^{\prime}$ involved in (1) the corresponding distances are related:
| $\operatorname{dist}(l,m)=\operatorname{dist}(l^{\prime},m^{\prime})\ \text{ and }\ \operatorname{dist}(l,l^{\prime})=\operatorname{dist}(m,m^{\prime}).$ | (2) |
1.A Theorem.
Relations (2) follow from (1).
Proof.
| $\operatorname{dist}(l,R_{m}\circ R_{l}(l))=2\operatorname{dist}(l,m)\text{ and }\operatorname{dist}(l^{\prime},R_{m^{\prime}}\circ R_{l^{\prime}}(l^{\prime} ))=2\operatorname{dist}(l^{\prime},m^{\prime}),$ |
therefore if $R_{m}\circ R_{l}=R_{m^{\prime}}\circ R_{l^{\prime}}$, then $R_{m}\circ R_{l}$ should move any line of the pencil by the same distance as $R_{m^{\prime}}\circ R_{l^{\prime}}$. Thus, $\operatorname{dist}(l,m)=\operatorname{dist}(l^{\prime},m^{\prime})$.
Further, by multiplying (1) by $R_{m^{\prime}}$ from the left and by $R_{l}$
from the right, we obtain $R_{m^{\prime}}\circ R_{m}=R_{l^{\prime}}\circ R_{l}$, from which the
second relation of (2) is deduced exactly as the first is deduced from
(1).
$\square$
Any three lines $l$, $m$, $l^{\prime}$ that belong to a pencil, can be supplemented by a unique line $m^{\prime}$ belonging to the same pencil such that the relations (2) are satisfied. (Of course, here the type of distance is determined by the type of the pencil.) Belonging of the lines to the same pencil and relations (2) imply (1).
Certainly, relations (1) are well-known. For example, in the group-theoretic approach to foundations of the classical geometries (see, e.g., the monograph [1] by Bachmann) lines were identified with reflections in them, belonging of three lines to a pencil of lines was defined as the fact that the composition of the corresponding reflections is a reflection. So, the relations (1) were turned into a definition of concurrency of three lines, that is belonging three lines to a pencil. We will call (1) pencil relations.
If $m=l$, then (2) implies $m^{\prime}=l^{\prime}$ and then (1) turns into $R_{l}^{2}=R_{l^{\prime}}^{2}$. The latter follows from the fact that reflections are involutions:
| $R_{l}^{2}=\operatorname{id}.$ | (3) |
We will call (3) involution relations.
1.3. Completeness of relations
Although the relations (1) and (3) are well-known, to the best of my knowledge, the following theorem has not appeared in the literature.
1.B Theorem.
Any relation among reflections in the group of isometries of Euclidean plane is a corollary of the pencil and involution relations.
1.C Lemma.
Any composition of four reflections can be converted by pencil and involution relations into a composition of two reflections.
Proof.
Assume that $k\cap l\neq\varnothing$ and $m\cap n\neq\varnothing$.
By rotating the pairs of lines $k,l$ and $m,n$ about the intersection
points, obtain pairs of lines $k^{\prime},l^{\prime}$ and $m^{\prime},n^{\prime}$ such that
$l^{\prime}=m^{\prime}$ is the line connecting the points $k\cap l$ and $m\cap n$.
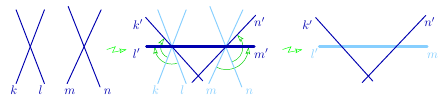
By the pencil relation, $R_{n}\circ R_{m}\circ R_{l}\circ R_{k}=R_{n^{\prime}}\circ R_{m^{\prime}}\circ R _{l^{\prime}}\circ R_{k^{\prime}}$, and, by the involution relation, $R_{m^{\prime}}\circ R_{l^{\prime}}=\operatorname{id}$. Hence, $R_{n}\circ R_{m}\circ R_{l}\circ R_{k}=R_{n^{\prime}}\circ R_{k^{\prime}}$.
Assume that $k\parallel l$ and $m\cap n\neq\varnothing$. Then translate $k\cup l$
to $k^{\prime}\cup l^{\prime}$ such that $l^{\prime}$ passes through $m\cap n$, and rotate $m\cup n$
about the point $m\cap n$ to $m^{\prime}\cup n^{\prime}$ such that $m^{\prime}=l^{\prime}$.
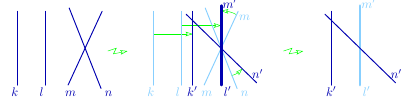
By the pencil relations, $R_{n}\circ R_{m}\circ R_{l}\circ R_{k}=R_{n^{\prime}}\circ R_{m^{\prime}}\circ R _{l^{\prime}}\circ R_{k^{\prime}}$, and, by the involution relation, $R_{m^{\prime}}\circ R_{l^{\prime}}=\operatorname{id}$. Hence, $R_{n}\circ R_{m}\circ R_{l}\circ R_{k}=R_{n^{\prime}}\circ R_{k^{\prime}}$.
If $m\parallel n$ and $k\cap l\neq\varnothing$, then we do the same, but exchanging the rôles of pairs $k,l$ and $m,n$.
Assume that $k\parallel l$ and $m\parallel n$, but $l\cap m\neq\varnothing$.
Then by rotating the middle pair of lines $l,m$ by right angle we obtain
the situation that was already considered: $k\cap l^{\prime}\neq\varnothing$ and
$m\cap n^{\prime}\neq\varnothing$.

The figure above provides also a proof of a well-known
fact that composition of translation is a translation by the vector which
is the sum of the vectors corresponding to the original translations.
If all the lines are parallel, then by a translation of $k\cup l$ such that
the image of $l$ would coincide with $m$ and applying pencil and involution
relations as above, we can reduce the number of reflections.
$\square$
Proof of Theorem 1.B.
Lemma 1.C provides an effective geometric simplification algorithm for evaluating a composition of reflections.
2. Isometries of the 2-sphere
2.1. Well-known facts
The group of isometries of the 2-sphere $S^{2}=\{x\in\mathbb{R}^{3}:|x|=1\}$ coincides with the orthogonal group $O(3)$: any isometry $S^{2}\to S^{2}$ is a restriction of linear orthogonal transformation of $\mathbb{R}^{3}$. In this section we prefer the language of isometries of $S^{2}$, but everything can be easily translated to the language of $O(3)$.
Classification. Any isometry of $S^{2}$ is either the identity $\operatorname{id}$, or a reflection $R_{l}$ in a great circle $l$ (i.e., the restriction of a reflection $\mathbb{R}^{3}\to\mathbb{R}^{3}$ in a 2-subspace), or a rotation about a pair of antipodal points (i.e., the restriction of a rotation $\mathbb{R}^{3}\to\mathbb{R}^{3}$ about a 1-subspace), or a glide reflection (the restriction of the composition of a rotation about a 1-subspace and the reflection in the orthogonal 2-subspace).
Generators. Any isometry of $S^{2}$ is a composition of at most three reflections in great circles.
Compositions of reflections. The composition $R_{m}\circ R_{l}$ of reflections in great circles $l$ and $m$ is
-
the identity if $l=m$;
-
a rotation about $l\cap m$ by the angle twice greater than the angle between $l$ and $m$ if $l\neq m$.
2.2. Relations among reflections
Any rotation can be presented as a composition of two reflections. The presentation is not unique. Any two great circles intersecting at the antipodal points fixed by the rotation and forming the required angle give rise to such a presentation.
This non-uniqueness of presentation can be formulated as relations among reflections in great circles. Each such relation involves four reflections and looks like this:
| $R_{m}\circ R_{l}=R_{m^{\prime}}\circ R_{l^{\prime}}$ | (4) |
where $l,m,l^{\prime},m^{\prime}$ are great circles such that $l\cap m=l^{\prime}\cap m^{\prime}$ and the angles between between the great circles satisfy two equalities: $\measuredangle(l,m)=\measuredangle(l^{\prime},m^{\prime})$, and $\measuredangle(l,l^{\prime})=\measuredangle(m,m^{\prime})$. Relations of this form are called the pencil relations, like similar relations in the isometry group of the Euclidean plane.
A reflection in a great circle is an involution, and we will refer to the relations $R_{l}^{2}=\operatorname{id}$ as to involution relations.
2.A Theorem.
In the isometry group of the 2-sphere, any relation among reflections follows from the pencil and involution relations.
2.B Lemma.
In the isometry group of the 2-sphere, any composition of four reflections can be converted by pencil and involution relations into a composition of two reflections.
The proofs of 2.B and 2.A repeat (with obvious simplifications) the proofs of 1.C and 1.B given above.
3. Special orthogonal group $SO(3)$
Special orthogonal group $SO(3)$ consists of linear maps $\mathbb{R}^{3}\to\mathbb{R}^{3}$ preserving distances and orientation. Each such map has eigenvalue 1, i.e., it has fixed line and rotates the whole 3-space about the line by some angle. Therefore it can be represented as a composition of two reflections in planes. (Notice that reflections in planes do not belong to $SO(3)$, because they reverse orientation.) The axis of rotation is the intersection of those planes, the angle between the planes is half the rotation angle.
3.1. Reflections in lines
The rotation by $180^{\circ}$ of the 3-space about a line $l$ is called the reflection in $l$. The notation $R_{l}$ is extended to reflections of this kind.
3.A Theorem.
A composition $R_{b}\circ R_{a}$ of reflections in lines $a$ and $b$ is the rotation by the angle twice greater than the angle between $a$ and $b$ about the axis $c$ which is perpendicular to $a$ and $b$.
Proof.
| $R_{b}\circ R_{a}=R_{B}\circ R_{C}\circ R_{A}\circ R_{C}.$ |
Since the reflections in orthogonal planes $C$ and $A$ commute,
| $R_{B}\circ R_{C}\circ R_{A}\circ R_{C}=R_{B}\circ R_{A}\circ R_{C}^{2}=R_{B} \circ R_{A}.$ |
As the composition of reflections in planes $A$, $B$ with $A\cap B=c$,
$R_{B}\circ R_{A}$ is a rotation about $c$ by the angle twice the angle
between $A$ and $B$. The angle between $A$ and $B$ equals the angle between
$a$ and $b$.
$\square$
3.2. Pencil relations
The representation of a reflection in a line provided by Theorem 3.A is non-unique. This non-uniqueness can be considered as relations among quadruples of reflections in lines. Namely, if $a$, $b$, $c$, $d$ are coplanar lines, $\measuredangle(a,b)=\measuredangle(c,d)$ and $\measuredangle(a,c)=\measuredangle(b,d)$, then
| $R_{b}\circ R_{a}=R_{d}\circ R_{c}.$ | (5) |
As (5) is similar to (1) and the four lines involved in (5) belong a pencil of lines, (5) is also called a pencil relation.
3.3. Polar frame relations
3.B Theorem.
If $a$, $b$ and $c$ are pairwise orthogonal lines in $\mathbb{R}^{3}$ passing through the origin, then $R_{b}\circ R_{a}=R_{c}$, or, equivalently and more symmetrically,
| $R_{c}\circ R_{b}\circ R_{a}=\operatorname{id}.$ | (6) |
Proof.
A relation (6) is called an polar frame relation.
3.4. Presentation of $SO(3)$
3.C Theorem.
The group $SO(3)$ is generated by reflections in lines, any relation in $SO(3)$ among reflections in lines follows from pencil, involution and polar frame relations.
3.D Lemma.
Any composition of three reflections in lines of $\mathbb{R}^{3}$ can be converted by polar frame, pencil and involution relations into a composition of two reflections in lines.
Proof.
By a polar frame relation, $R_{k}=R_{c}\circ R_{b}$, and hence
$R_{m}\circ R_{l}\circ R_{k}=R_{m}\circ R_{l}\circ R_{c}\circ R_{b}$. Now, lines $c$, $l$
and $m$ are coplanar, and by a pencil relation their composition
$R_{m}\circ R_{l}\circ R_{c}$ is a reflection in a line.
$\square$
Proof of Theorem 3.C.
Take any relation $R_{1}\circ R_{2}\circ\dots\circ R_{n}=\operatorname{id}$ among reflections
in lines.
By Lemma 3.D, we may reduce its length $n$ by applying
polar frame, pencil and involution relations to a number which is less than
three.
The composition of two reflections in non-coinciding lines is a rotation by
the angle twice the angle between the lines. Thus, if the lines do not
coincide, then the composition is not the identity. If the lines coincide,
then the composition is the identity, but the relation is reduced to an
involution relation.
A relation cannot consist of a single reflection in a line, because a
reflection in a line is not identity.
$\square$
3.5. Orientation preserving isometries of the sphere
Elements of $SO(3)$ are orientation preserving isometries of $\mathbb{R}^{3}$. Their restrictions to the 2-sphere $S^{2}$ are orientation preserving isometries of $S^{2}$. Therefore the results of this section admit reformulations for the group of orientation preserving isometires of the 2-sphere. In particular, Theorem 3.C means that this group is generated by reflections in pairs of antipodal points and any relation among such reflections follow from the corresponding versions of pencil, involution and polar frame relations.
This is in a sharp contrast to the situation in the group of orientation preserving isometries of the Euclidean plane, in which the only involutions are reflections in points, and they do not generate the group. The group generated by all the involutions consists of the involutions themselves and all the translations.
3.6. Isometries of the projective plane
Consider the projective plane $\mathbb{R} P^{2}$ equipped with the metric defined by the Euclidean metric in $R^{3}$. The isometry group of the projective plane is $PO(3,\mathbb{R})$. Each isometry $\mathbb{R} P^{2}\to\mathbb{R} P^{2}$ admits two liftings to the covering space $S^{2}$. The two liftings differ by the antipodal involution of $S^{2}$, the only non-trivial automorphism of the covering $S^{2}\to\mathbb{R} P^{2}$. The antipodal involution of $S^{2}$ reverses orientation. Therefore one of the liftings of any isometry of $\mathbb{R} P^{2}$ is orientation reversing and the other one is orientation reversing.
The fixed point set of an isometry-involution of the projective plane consists of a point and a line polar to each other. Its lifting reversing orientation is a reflection in a great circle, while the lifting preserving orientation is a reflection in a pair of antipodal points. The great circle and the antipodal points cover the components of the original involution of the projective plane.
The construction of orientation preserving covering map defines an isomorphism of the group of isometries of the projective plane to a group of orientation preserving isometries of the 2-sphere.
Therefore Theorem 3.C implies that the isometry group of the projective plane is generated by involutions and any relation among the involutions of the projective plane is a corollary of relations that correspond to pencil, involution and polar frame relations.
4. New graphical calculus for rotations
4.1. Arrow-arcs presenting a rotation
Any orientation preserving isometry of $S^{2}$ is a rotation about a line $l\in\mathbb{R}^{3}$, or, if we want to speak solely in terms of $S^{2}$, a rotation about the set $l\cap S^{2}$ of two antipodal points. By Theorem 3.A, it is a composition of reflections in lines $a$ and $b$ orthogonal to $l$. On $S^{2}$, these reflections are represented by two-point sets $a\cap S^{2}$ and $b\cap S^{2}$. There is a natural ordering of the sets: if the rotation is represented as $R_{b}\circ R_{a}$, we have to apply $R_{a}$, first, and $R_{b}$, second. Thus, $a$ precedes $b$.
A two-point set consisting of antipodal points can be recovered from any of its points. Let us pick up a point $A$ from $a$ and a point $B$ from $b$ and form an ordered pair $(A,B)$. The pair $(A,B)$ encodes $R_{l}$. In order to make $(A,B)$ more visible, let us connect them with an arc equipped with an arrow. The angular length of the arc is half of the angle of the rotation.
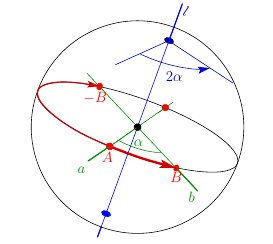
Figure 2. Arrow-arc ${AB}$ represents a rotation by $2\alpha$.
By pencil relations, an arrow-arc representing a rotation is defined by the rotation up to gliding along its great circle and replacing the arrowhead by the antipodal point.
This representation of rotation reminds the traditional representation of a translation by an arrow. However, there are two important differences.
First, an arrow representing a translation connects a point with its image under the translation, while in an arrow-arc representing a rotation the arrowhead is on the half a way to the image of the arrowtail.
Second, the image under any translation of an arrow representing a plane translation still represents the same translation, while an arrow-arcs representing the same rotation are locked on the same great circle.
Since a translation can be represented as a composition of two symmetries with respect to points, a translation can be also represented by an arrow connecting the centers of symmetries. This representation of translations differs from the traditional one just by the length of the arrows: the traditional arrows are twice longer. Despite this rescaling, it has all advantages of the traditional one.
4.2. Triangle rule for arrow-arcs
Usually a rotation of $\mathbb{R}^{3}$ is presented by so called angular displacement vector. This is an arrow directed along the axis of rotation, its length is the angle of rotation and the direction is defined by some orientation agreement (a right-hand rule). A well-known drawback of angular displacement vector is that it has a complicated behavior under composition of rotations: the angular dispalcement of a composition of rotations $U$ and $V$ is not the sum of the angular displacements of $U$ and $V$, although it is defined by the angular displacements of $U$ and $V$. The relation between the angular displacement of $V\circ U$ and the angular displacements of $U$ and $V$ is too complicated to be useful.
The arrow-arc representation of $V\circ U$ can be easily calculated in terms of arrow-arcs for $U$ and $V$.
4.A Theorem.
Let rotations $U$ and $V$ of $S^{2}$ be represented by arrow-arcs $AB$ and $CD$, respectively. The great circles containing the arcs intersect (as any two great circles). By sliding the arrow-arcs along their great circles, one can arrange them so that $B=C$. Assume this has been done. Then the rotation $V\circ U$ is represented by the arrow-arc $AD$.
Proof.
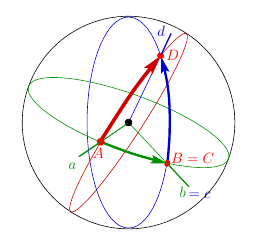
Figure 3. The sum of arrow-arcs represents the composition of rotations represented by the summands.
5. Orthogonal groups $O(n)$
5.1. Well-known facts
Any orthogonal linear transformation $T:\mathbb{R}^{n}\to\mathbb{R}^{n}$ splits into orthogonal direct sum of orthogonal transformations of 1- and/or 2-dimensional spaces. See, e.g., [2], 8.2.15. On a 1-dimensional subspace an orthogonal transformation is either identity or symmetry in the origin. Therefore $T$ splits into orthogonal direct sum of a reflection in a vector subspace and rotations of 2-subspaces.
This orthogonal sum splitting of $T$ can be turned into a splitting of $T$ into a composition. For this, extend the transformation on each summand to a transformation of the whole space by the identity on the orthogonal complement to the summand. The extended transformations of the whole space commute with each other and their composition equals the original transformation.
Since a rotation of plane is a composition of two reflections in lines, it follows that any element of $O(n)$ can be represented as a composition of reflections in hyperplanes. Any element of $O(n)$ can be represented as a composition of at most $n$ reflections. See, e.g., [2], 8.2.12.
5.2. Pencil relations among reflections
Non-uniqueness for representation as a composition of two reflections for a plane rotation implies non-uniqueness for representation of a rotation of $\mathbb{R}^{n}$ about a subspace of codimension 2 as a composition of two reflections in hyperplanes.
As in Section 1.2, this non-uniqueness can be formulated as relations among reflections in hyperplanes. We will call these relations also pencil relations.
5.A Theorem.
In $O(n)$ any relation among reflections in hyperplanes follows from pencil and involution relations.
A proof of Theorem 5.A is similar to the proof of Theorem 1.B above and is based on the following lemma:
5.B Lemma.
In $O(n)$, any composition of $n+1$ reflections in hyperplanes
can be converted by pencil and involution relations
into a composition of $n-1$ reflections in hyperplanes. $\square$
References
- 1 Friedrich Bachmann, Aufbau der Geometrie aus dem Spiegelungsbegriff, Springer-Verlag, 1973.
- 2 Marcel Berger, Geometry I, Springer, 2009.