1. Graph the rational function y=(x+1)/(x2+2x-3). Find asymptotes and intercepts.
2. Evaluate a) eln(35) b)
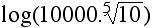
3. Sketch the graph of y=4x
4. Solve for x: 3 log x = log x + log (2+x)
5. Compute all six trigonometric functions of t, if cos t=1/4 and t is in the fourth quadrant.
6. prob 8. pag 387
7. Sketch the graph of the polynomial function
y=x3+x2-x-1. Make sure that your graph shows all intercepts and exhibits the proper end behavior.
8. Use the Laws of Logarithms to rewrite the expression in a form with no logarithm of a product, quotient root or power. a) ln(3y2/(x-6)2) b) loga(a2/bcd4)
9. Find a function of the form y=c ax whose graph passes
through the point (1,6) and intercepts the y-axes in y=2.
10. Solve for x: a. ex+7=e2e2x+1 b. e2x - ex - 6=0
11. Compute the all six trigonometric functions of t, if sin t=-1/2 and t is in the thrid quadrant.
12. prob 3 pag 386