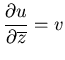COMPLEX ANALYSIS II


Fall Semester 2001


Blaine Lawson

TOPICS TO BE COVERED

NOTE: The first class will be on Tuesday September 11.


0. Review. The Cauchy kernel, solving 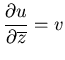$ {\displaystyle \frac{{\partial}u}{\partial \overline z}=v}$, estimates, power series, removable singularities.


1. The Runge Approximation Theorem


2. The Mittag-Leffler Theorem


3. The Weierstrauss Factorization Theorem


4. The $ \Gamma$ function; the Riemann zeta function


5. Elliptic Functions- the Weierstrauss $ {\mathfrak{p}}$-function


6. The Schwarz relection principle, analytic continuation


7. Algebraic functions, the Weierstrauss Preparation Theorem


8. Riemann surfaces


9. Harmonic and subharmonic functions


10. Entire functions: Jensen's formula, the Shottky and Picard Theorems, some value distribution theory