|
|
 
Tiling the Plane |
|
|
 
Tiling the Plane |
|
What is the plane? Our conception of the plane comes from the seventeeth century philosopher mathematician, René Descartes (you can read more about Descartes in the Internet Encyclopedia of Philosophy). One day, or so the story goes, Descartes was lying on his bed when he saw a fly crawling across the ceiling. He started wondering how he could describe the fly's position. He came up with the idea of a rectangular co-ordinate system: you fix a set of perpendicular axes, and then label any point on the ceiling by reading its numbers off the axes, something like this:

The point indicated is labelled (4,3). The term plane refers to any flat two dimensional surface like a ceiling, a piece of paper, a table top or a cutting board, only an abstract mathematical plane has no boundary; it goes on forever. Notice that to fix a point in this two-dimensional space, we need exactly two numbers.
We are interested in covering the plane in interesting ways. Think
of it as coloring-in for grown ups.
Before we get to covering the whole plane, let's start off with just a square. To do this exercise, you'll need a piece of paper and some colored pens. On your piece of paper, draw a pretty big square in black. Now, still using black, draw a whole lot (at least seven or eight) of straight lines inside your square. The lines have to go from one side of the square's perimeter to the other. Here's an example:
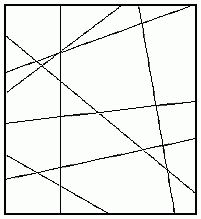
You now have to color-in the square using as few colors as possible, but making sure that no adjacent regions are the same color (by adjacent I mean sharing a common edge, not a common vertex.) What is the minimum number of colors needed? The above exercise is a very easy example of what turned out to be a very difficult problem, called the Four Colored Problem: What is the minimum number of colors needed to color-in any map so that no touching areas are the same color?As you might guess from the name of the problem, the answer turned out to be four! The first proof of this relied heavily on computers. It was one of the first mathematical "proofs by computer" ever given, and this generated a good deal of controversy. (Why would a "proof by computer" generate mathematical controversy?) Find a black and white map of your country showing only the borders between states or provinces. Color-in the map using only four colors so that no two touching areas are the same color. Try the same task on a map of South America (a map showing only the borders between countries). How about Europe? How about Africa? Which continent is the hardest to do? You can read more about the four color problem in the CRC Concise Encyclopedia of Mathematics and in Ivars Peterson's Mathland. Now that we've looked at one of the most famous problems about coloring plane figures let's turn our attention to the whole plane. It is easy to cover (or tile) the plane using shapes like rectangles or squares, or even hexagons and dodecahedrons. You can check out a website which shows a host of tilings by pentagons. In fact there are many cool shapes which tile the plane giving nice symetric patterns, a concept which the artist M. C. Escher used very well. (You can check out lots of cool Escher sites on the web, like the World of Escher, and the electropolis site which has lots of pictures.) Notice how many of these tilings create repeating patterns. In 1974, Roger Penrose, a math professor at Oxford (you can read more about him at the World of Escher site) solved the following problem: What is the smallest number of different tiles needed to cover the plane without creating a repeating pattern?Try it. Cut out different shapes. See what you can do. Then check out the Official Answer. You can also play an interactive tiling the plane game at the site hosted by the Shodor Education Foundation. 
|