The Golden Mean

The Ancient Greeks were much concerned with harmony, with things being in correct proportion and relation to one another. They took great care,and this can be seen in their art and architecture.

The golden mean is sometimes also called the golden ratio. What is a ratio? A ratio is a formula for dividing a given whole into separate parts. For example, if we have to divide some given amount in the ratio 2:3 (we say the ratio two-to-three), we take the amount we are given and divide it up into blocks of 5 (where does 5 come from?) Each block of 5 can then be divided up into a parcel of 2 and a parcel of 3. Collecting all of the parcels of 2 together and all of the parcels of 3 together divides the original amount in the ratio 2:3.

Let me make this a little more concrete. Suppose we have a bag of 50 sweets, and suppose that Rachel and Thandi have to divide the sweets among themselves in the ratio 2:3 (Thandi has been good this year, while Rachel likes to bite her baby brother). Dividing 50 by 5 gives us 10 blocks of 5. From each of these blocks of 5 sweets, Rachel gets 2 sweets and Thandi gets 3, so that Rachel gets 20 sweets and Thandi 30.

Divide the following amounts into the indicated ratios.

21 by the ratio 4:3
65 by the ratio 1:7
81 by the ratio 2:3:4

What do you think should happen to the remainder when you divide 65 into the ratio 1:7?

Notice that ratios behave like fractions. The ratio 2:3 and the ratio 4:6 are the same thing, just like the fraction 2/3 and the fraction 4/6 are the same.

Now that we know about ratios, we can consider the golden ratio, or golden mean. The golden ratio was considered by the Ancients to be the perfect way of dividing a whole up into parts. What do you think "perfect" means in this context? Do you think there can be a "perfect" way of divding something up?

For the Ancients, perhaps the most important criterion for perfection was aesthetic. They wanted things to look good! Draw a line on a piece of paper, and consider ways of dividing this line into two segments. What do you think is the most aesthetically pleasing way of doing this?

There is no right answer to this question of course. I bet many of you chose the midpoint of the line as the best place for division. I think that's a perfectly good answer (although my opinion doesn't mean much to anyone but me!)

Let's look at another "good" answer. Suppose you want to divide the line so that the ratio of the larger section to the smaller section is the same as the ratio of the the whole line to the larger section.

Let's give things some names. Suppose the length of the larger section is l and the length of the smaller section is s. Then the length of the whole is l+s. We want:

l:s to be the same as l+s:l

l/s = (l+s)/l

Let's give the ratio l/s a name. For the moment, I'll use G (any guess why?). Then

G = l/s = (l+s)/l = 1 + s/l = 1 + 1/G

That is to say,

G = 1 + 1/G

G ² - G - 1 = 0

The positive root of this equation is

(1 + the square root of 5)/2

This number is defined to be the golden mean (or ratio) and it is usually denoted not by G but by the greek letter f (phi).

Is f rational or irrational (check out the analysis page if you don't know what these words mean). Can you prove this?

Now, let's look at something completely different: the Fibonacci sequence. (You should read more about sequences before going on.)

The first term of the Fibonacci sequence is 1, and so is the second. The third term is 2 and the fourth term is 3. The fifth term is 5. Can you guess what the sixth term is? Can you see the rule for generating more terms in this sequence? When you've thought about it, check out the official rules for the Fibonacci sequence.

Next, I want to look at another kind of sequence, one called a continued fraction. Here is an example. Let the first term in our sequence be 1/1. Let the second term be 1 + 1/1. The third term is 1 + 1/(1+1). The fourth term is 1 + 1/[1 + 1/(1 + 1/1)]. A picture makes things clearer: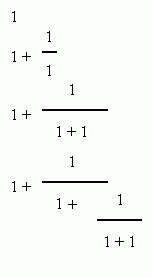

Can you see a connection between the Fibonacci sequence and the continued fraction in the above example?

Let's return to the equation that we generated in defining the golden mean:

G = 1 + 1/G

except we'll use f now that we know what G is

f= 1 + 1/f

Notice how this allows us to define f in terms of itself. This kind of thing is called a recursive relationship:

f= 1 + 1/f
f= 1 + 1/(1 + 1/f)
f= 1 + 1/(1 + 1/[1 + 1/f])

and so on. What happens if we carry on this process indefinitely? We get the infinite continued fraction

f= 1 + 1/[1 + 1/[1 + 1/[1 + 1/[ ....

Does this look familiar?

Can you prove that the limit of the sequence of ratios of successive Fibonacci numbers is the Golden mean?

In fact, there are many different and interesting formulae for the golden mean. As a project, how many of them can you find? (Here are some clues: there is a formula for the golden mean involving infinitely continued radicals. Also, a famous mathematician called Ramanujan did lots of work in number theory, including some on the golden mean. You can read more about Ramanujan in the the MacTutor History of Mathematics Archive.)