PROBLEM OF THE MONTH
March 2004
Consider a polygon, P, drawn in the Euclidean plane such that all of
the vertices of P have integer coordinates. That is, if we think of the
plane as a giant sheet of graph paper, the vertices of the polygon all
lie on the lattice points of the paper. The area
of the polygon can be computed by counting the number of lattice
points inside the polygon and the number of lattice points on the edge
of the polygon. Let
I = the number of lattice points inside P
and
E = the number of lattice points along the edges of P, including
the vertices.
Then the area, A, of P is given by the formula: A = I + E/2 - 1
For example, for the irregular hexagon below, I=13 and E=9. So
our formula predicts that the area of the polygon should be:
13 + 9/2 -1 = 16 1/2.
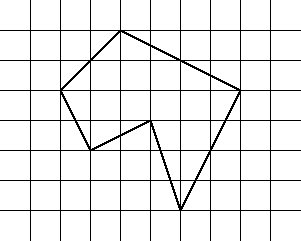
We can check our result by computing the area of the polygon.
Breaking P into triangles and rectangles,
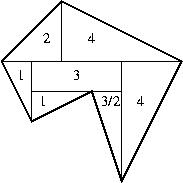
we see that the area is:
2 + 4 + 1 + 3 + 4 + 1 + 3/2 = 16 1/2.
PROBLEM:
- Prove that the formula for the area of P is correct for any triangle.
- Prove that the formula for the area of P is correct for any polygon,
regardless of the number of sides.
Submit your solution to the Mathematics Undergraduate Office (Math P-142)
or electronically to Prof. Kudzin at
problem@math.sunysb.edu
by the due date. Acceptable electronic formats are: PDF, Postscript, DVI,
(La)TeX, or just plain text. Please include your name and phone number,
or preferably your email address.
Closing date: April 15th at 12 pm.


