Hex is a board game for two players, who we will call "Black" and "White". The game is played on an n x n grid of hexagons. Two opposite edges of the board are labeled "Black". The other two edges are labeled "White". Black plays first. Each player, on his turn, places a stone of his color on any unoccupied hexagon. A stone, once placed, is never moved or taken off of the board. The first player to form an unbroken chain of stones connecting the two appropriately labeled edges wins the game.

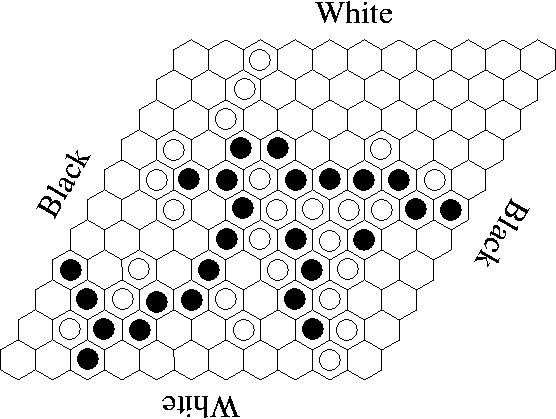
The diagram below illustrates a game, played on an 11x11 board, which Black has just won.

Hex has two important properties.

1. The game can never end in a draw. By the time the board is filled with stones, one player or another will have formed a winning chain.
2. There is never any disadvantage in having an extra piece on the board or being forced to make a move.

THEOREM: With perfect play, Black can always win.

The idea of the proof is the following. There are no random or unknown elements affecting the game; no rolling dice, no cards hidden from view. In that respoect, Hex is more like checkers or chess than it is like yahtzee or poker. In poker, you can always lose, no matter how skillfully you play, if you are unlucky. However, in Hex, luck is not a factor. Therefore, since the game cannot end in a draw, there must be a strategy for one of the players which will guarantee victory. The question is, which player has the winning strategy?

Assume that White, the second player, has a winning strategy. If so, then Black could "steal" White's strategy as follows: Black, on his first turn, makes a random move. He now "forgets" about the stone he just placed, and pretends like White is the first player. He uses White's strategy, playing as if he never made his first move. By the second property, he can never be hurt by the additional stone he has placed on the board. If his strategy ever requires him to play on the hexagon where he first moved, then he just makes another random move and then "forgets" that he made it. Now, both Black and White have a strategy which guarantees victory, which is clearly impossible, so White cannot have a winning strategy. Thus it must be Black which has the winning strategy.

Notice that this theorem does not explain what Black's winning strategy is. Rather, it just says that there has to be one. People have worked out explicit strategies when the board is small enough (7x7 or smaller). When the board is larger, nobody knows what the correct strategy is. In actual play, both sides have reasonably good chances to win.

Although we don't know what Black's strategy is, we do know what it isn't. Your challenge for this month is to prove the following:

PROBLEM: On any sized board, 2x2 or bigger, if Black places his first stone in one of the two "acute" corners (the upper right or bottom left in the figure above), then he has thrown away the advantage that he had by going first, and it is now White who has a winning strategy.