Jonathan Inbal provided the following solution:

THEOREM:An n x n square can be cut into "T" tetraminos if and only if n is divisible by 4.

In particular, a 10 x 10 square cannot be cut into "T" tetraminos.

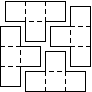
PROOF: First, notice that a 4 x 4 square can be made out of "T" tetraminos as follows:

Conversely, assume that the square can be cut into "T" tetraminos. Since each tetramino consists of 4 squares, the square must be cut into n²/4 tetraminos. Since this number must be an integer, n² is divisible by four which implies that n is divisible by 2. Now, color the squares black and white in a checkerboard pattern

1. Since n is even, exactly half of the squares are black and half are white. Therefore there are n²/2 white squares.
2. Let w be the number of tetraminos composed of three white squares and one black square. The number of tetraminos composed of three black squares and one white square is n²/4 - w, so there are a total of 3*w + 1*(n²/4 - w) white squares.

This proof can be modified to provide some information in the case of an m x n rectangle. It can be shown that a necessary condition for the rectangle to be cut into "T" tetraminos is that the area, mn, must be divisible by 8. However, this condition is not sufficient, since a 1 x 8 rectangle can clearly not be subdivided. A sufficient condition is that both m and n be divisible by 4. Mr. Inbal has conjectured that this condition is also necessary. It would be interesting to try to prove his conjecture.