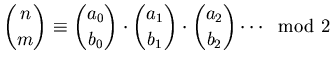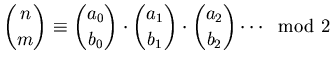PROBLEM OF THE MONTH
November 2002
Let 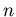 and
and 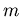 be two positive integers, with
be two positive integers, with 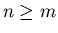 , and let
, and let
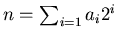 and
and
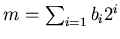 be their binary
expansions (i.e.
be their binary
expansions (i.e. 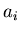 and
and 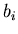 are the digits of
are the digits of 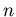 and
and 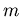 in base
in base 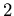 )
)
- Show that the following congruence holds
(Here
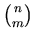 denotes the corresponding binomial coefficient,
that is the coefficient of
denotes the corresponding binomial coefficient,
that is the coefficient of 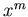 in
in 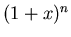 . Alternatively, binomial coefficients
. Alternatively, binomial coefficients
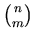 are sometimes denoted by the symbols
are sometimes denoted by the symbols
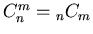 , usually when interpreted as the
``number of combinations of
, usually when interpreted as the
``number of combinations of 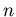 objects
taken
objects
taken 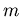 at a time''. By convention,
at a time''. By convention,
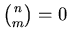 if
if 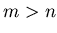 .)
.)
- Can you use the first part to say when
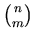 is odd? For
what
is odd? For
what 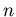 is
is
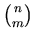 odd for all
odd for all
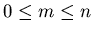 ?
?
- Can you give a simple description of the largest power of
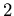 dividing
dividing
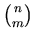 ?
?