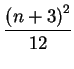PROBLEM OF THE MONTH
SEPTEMBER 2001
 , 2-cent
, 2-cent  , and 3-cent
, and 3-cent  stamps?
stamps?
In making up ![]() cents out of
cents out of ![]() ,
, ![]() and
and ![]() -cent stamps, we can use
either no
-cent stamps, we can use
either no ![]() -cent stamps at all, or up to
-cent stamps at all, or up to
![]() of them. (Here and in the sequel
of them. (Here and in the sequel
![]() denotes the largest integer smaller than
denotes the largest integer smaller than ![]() .)
In the first case the
.)
In the first case the ![]() cents would have to be made up out of
cents would have to be made up out of
![]() and
and ![]() -cent stamps, and this cane be done in
-cent stamps, and this cane be done in
![]() different ways. This is easy to see:
the number of used
different ways. This is easy to see:
the number of used ![]() -cent stamps can't exceed
-cent stamps can't exceed
![]() ,
and then the rest of the amount has to be made up out of
,
and then the rest of the amount has to be made up out of ![]() -cent stamps, so there are
-cent stamps, so there are
![]() ways to make up
ways to make up ![]() cents out of
cents out of ![]() and
and ![]() -cent stamps
only.
-cent stamps
only.
If say we now use only one ![]() -cent stamp, then the remaining
-cent stamp, then the remaining ![]() cents will have to be made up
of
cents will have to be made up
of ![]() and
and ![]() -cent stamps, and as above this can be done in
-cent stamps, and as above this can be done in
![]() different ways. And so on, if we now use only two
different ways. And so on, if we now use only two ![]() -cent stamps, then the
remaining
-cent stamps, then the
remaining ![]() cents will have to be made up of
cents will have to be made up of ![]() and
and ![]() -cent stamps, and again
this can be done in
-cent stamps, and again
this can be done in
![]() ways.
ways.
Finally, if we use the maximum allowed number
![]() of
of ![]() -cent stamps, then the remaining
-cent stamps, then the remaining ![]() cents will have to be made
up out of
cents will have to be made
up out of ![]() and
and ![]() -cent stamps and there are
-cent stamps and there are
![]() ways to do that (
ways to do that (![]() is the remainder of the division of
is the remainder of the division of ![]() by
by ![]() and so
and so ![]() , or
, or ![]() ).
).
Therefore we get a total of
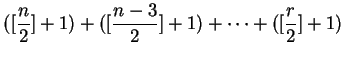
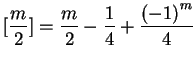
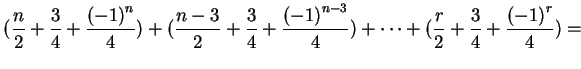
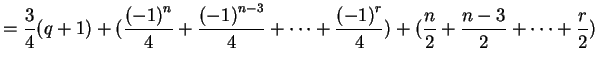
The terms in the first sum alternate in sign, so this parenthesis is
![]() if
both
if
both ![]() and
and ![]() are even, -
are even, -
![]() if both are odd, or 0 otherwise. We will
denote this sum by
if both are odd, or 0 otherwise. We will
denote this sum by ![]() . On the other hand, the terms in the second sum form an arithmetic progression.
In conclusion we obtain that there are
. On the other hand, the terms in the second sum form an arithmetic progression.
In conclusion we obtain that there are
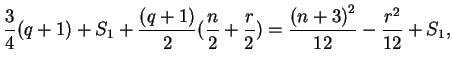
It is easy to see that the above obtained expression represents in fact the nearest integer to