PROBLEM OF THE MONTH
OCTOBER 2001
Let X be a region in the plane with area strictly greater then one.
Show that X contains two at least two distinct points
with coordinates (a,b) and (c,d) such that
a-c and b-d are both integers.
Cover the plane with non overlapping squares of edge one, whose lower left corners are points with integer
coordinates. More precisely, use the squares 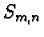 with lower left corners
with lower left corners
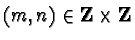 where
where
The region 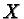 is then decomposed into pieces
is then decomposed into pieces
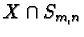 by the squares
by the squares 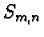 . Denote by
. Denote by 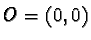 the
origin and translate each square
the
origin and translate each square 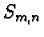 along the segment joing
along the segment joing 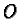 and
and 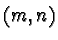 so that all squares are superimposed onto
so that all squares are superimposed onto 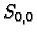 . The
pieces
. The
pieces
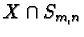 are therefore translated onto subsets
are therefore translated onto subsets 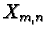 of the square
of the square 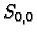 .
The total area of all these pieces is the area of
.
The total area of all these pieces is the area of 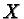 which is assumed to be greater than one
(
which is assumed to be greater than one
(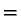 the area of the square
the area of the square 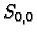 ), hence at least two such translates must meet. Let
), hence at least two such translates must meet. Let 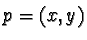 be a point
which is both in
be a point
which is both in 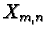 and
and 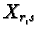 with
with
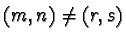 . It follows that the point
. It follows that the point
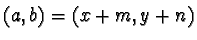 lies in
lies in
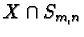 , while
, while
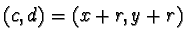 lies in
lies in
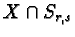 .
Thus both
.
Thus both 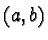 and
and 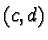 lie in
lie in 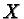 , and furthermore
, and furthermore 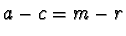 and
and 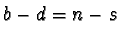 are both integers.
are both integers.
The simple way to phrase what we have just proved is that if 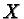 is a region in the plane with area
greater than one, then there exist a point
is a region in the plane with area
greater than one, then there exist a point 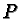 with integer coordinates such that
with integer coordinates such that 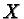 and its translate
along the segment
and its translate
along the segment 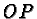 have a point in common.
have a point in common.
![]() with lower left corners
with lower left corners
![]() where
where
![]() is a region in the plane with area
greater than one, then there exist a point
is a region in the plane with area
greater than one, then there exist a point ![]() with integer coordinates such that
with integer coordinates such that ![]() and its translate
along the segment
and its translate
along the segment ![]() have a point in common.
have a point in common.