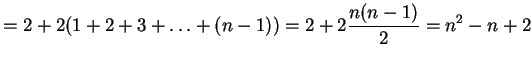
PROBLEM OF THE MONTH

APRIL 2001


 






What is the greatest number of parts the plane can be divided by:
  • n straight lines ?
  • n circles ?

For instance, the following two drawings visualize the cases of 4 lines and of 3 circles, respectively:

The above 4 lines divide the plane in 11 regions The above 3 circles divide the plane in 8 regions

a) It is clear that $ n$ lines will divide the plane into a maximum number of regions if any two of these lines actually intersect and no three of them are concurrent. In other words we have to determine into how many regions $ n$ mutually non-parallel lines, no three of which are concurrent, divide the plane. Denote this number by $ p(n)$. Direct observation leads to the first values of this number:

$\displaystyle p(1)=2,\qquad p(2)=4,\quad {\textrm {etc}}. $

Suppose that $ n-1$ lines have already been drawn in the plane and let us count by how much it increases the number of regions when we draw the $ {n}^{\textrm {th}}$ line. The $ {n}^{\textrm {th}}$ line meets all the previous lines and the $ n-1$ points of intersection with them divide this new line into $ n$ parts. In other words the $ {n}^{\textrm {th}}$ line cuts exactly $ n$ of the regions into which the plane has already been divided. Since it splits each of these regions into two pieces we get that

$\displaystyle p(n)=p(n-1)+n, \qquad {\textrm {for all}}\quad n\ge 2$

Since $ p(1)=2$ we obtain that

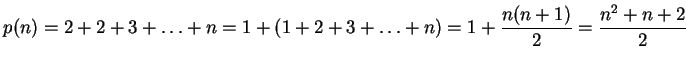
$\displaystyle p(n)=2+2+3+\ldots+n=1+(1+2+3+\ldots+n)= 1+\frac{n(n+1)}{2}=\frac{n^2+n+2}{2} $


b) The second part of the problem is very similar to the first one. Namely, $ n$ circles will divide the planes into a maximum number of regions if every two of them intersect (that is, if no two of them are tangent and none of them lies entirely within or outside of another one) and no three of them are concurrent. Reasoning similarly to the first part, we see that the circle intersects each of the first circles in two points. These points divide the circle into arcs. Each of these arcs divides into two one of the regions formed by the first $ n-1$ circles. Since one circle divides the plane into two regions we get as above that the total number of regions after drawing the $ {n}^{\textrm {th}}$ circle is

$\displaystyle 2+2+4+6+8+\ldots+2(n-1)=$

$\displaystyle =2+2(1+2+3+\ldots+(n-1))=2+2\frac{n(n-1)}{2}= n^2-n+2$