| Through Mazes |
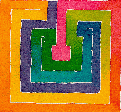 |
to Mathematics |
| Through Mazes |
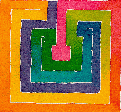 |
to Mathematics |
Proposition. (Jim Reeds; see also Lando and Zvonkin (1992)) If n is a power of a prime number p then M(2n) is congruent to (~) 2 mod p.
Examples: M(4) = 2 ~ 2 (mod 2); M(6) = 8 ~ 2 (mod 3); M(10) = 262 ~ 2 (mod 5); M(26) = 6405031050 ~ 2 (mod 13), etc.
Proof: Write each maze as a chord diagram with vertices on 2n points. The group Z_2n then acts on the set of mazes by cyclic shifts to the left. The order of any orbit must be a divisor of 2n: either 1, 2, or a multiple of p. Since n > 1 there are no orbits of order 1 (fixed points), and there exists a (unique) orbit of order 2, corresponding to the top chord diagram illustrated. The sum of the orders of the orbits must be M(2n); the proposition follows.
Proposition. (Lando; see Lando and Zvonkin (1993)) M(n) is odd if and only if n = 2^k + 1.
Examples: the only M(2^k + 1) known are M(2,3,5,9,17); these are also the only odd M's known. If M(33) is ever calculated, it will be an odd number.
Proof: First note that M(2n+1)~M(n+1) (mod 2). This is checked by
examining the relation of
duality on maze-paths of depth 2n+1. The
non-self-dual mazes are paired off two by two; in a self-dual maze,
the maze path can only cross the line separating levels n and n+1
once (otherwise self-duality would force the existence of a
closed sub-maze); this line splits the maze into two mirror-image
mazes of depth n+1; each maze of depth n+1 gives a unique self-dual
maze of depth 2n+1 by reversing this procedure. So M(1+1)=1
=> M(2+1)~1 => M(4+1)~1 etc. On the other hand every M(2n)
is even: there is a non-trivial involution on the set of
chord diagrams which interchanges
red and blue chords; and every M(2n+1) which is not of the
form M(2^k+1) is eventually congruent to an M(even).
Return to Main Maze Page
Return to Tony's Home Page