The int command is used to compute both definite and indefinite
integrals of Maple expressions. Its syntax is basically
>
int(f,x);
where f is an algebraic expression and x is the integration
variable. For example, to compute
>
int((3*x-6)/(x^2-4),x);
![]()
Notice that Maple does not provide the constant of integration. You will
occasionally have to take this into account and provide your own constant.
You must specify the variable of integration. In expressions involving other
parameters, Maple assumes that you want the integral of the expression as the
variable you specify changes and that all other parameters in the expression
represent constants:
>
int(exp(a*x),x);
![]()
To compute a definite integral, the range over which the integration
variable moves must be specified:
>
int(x^2*exp(x),x=0..2);
![]()
The int command in Maple has a particular behavior in certain
situations:
> int(ln(sin(sqrt(x^12-5*x^7+50*x+2))),x);
> int(sin(2*x)/x,x);
Si is the special name of one of these functions which appear
frequently in mathematical physics. To learn more about it, ask Maple
for help on it with the command ?Si. This will bring up a
window with information about the function Si.
If Maple responds to an integral with one of these functions, it is quite
likely that the integral cannot be evaluated in terms of elementary functions.
>
int(1/(x^8 +1),x);
![]()
In this answer, the sum is taken over all roots R of the polynomial
1 + 16777216z8, and the summand is
R log(x+8R).
As with diff, there is an inert form Int of the integral
command which can be used in combination with int to produce easily
readable worksheets:
>
Int(ln(1+3*x), x=1..4);
![]()
>
Int(ln(1+3*x), x=1..4)=int(ln(1+3*x),x=1..4);
![]()
The inert form Int is also very useful in many situations when
you wish to delay the evaluation of an integral, as we shall see
below.
evalf command, you can force Maple to apply a numerical
approximation technique for definite integration:
> evalf(Int(sqrt(1+x^10),x=0..1));
Int. This prevents Maple from attempting to evaluate
the integral symbolically and then applying evalf to the
answer. In many cases, this can save a huge amount of time, because
Maple will work very hard to try to compute the symbolic form of the
integral. For example, approximating
> evalf(int(exp(sin(x))),x=0..1);took more than 10 times the amount of time needed to execute
> evalf(Int(exp(sin(x))),x=0..1);More complicated integrals can have even more dramatic differences.
student and you must load
this library into computer memory before you can use it:
> with(student):
Once loaded, you can play with it. For example, if you want to use the
left sum approximation to an integral, the height of each rectangle is
determined by the value of the function at the left side of each
interval. You may specify the number of intervals you wish to use. If
you do not, Maple will use four intervals by default:
>
leftsum(x^4*ln(x),x=1..4,10);
![]()
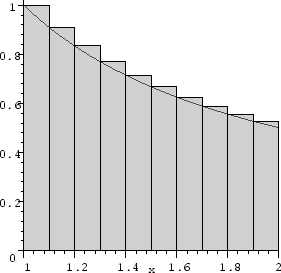
Maple can also draw pictures of the rectangles used to approximate the integral
of a function on a given interval:
>
leftbox(1/x,x=1..2,10);
The following is the result of using the Simpson's rule for the function
xsin(x2) on the interval
1 ![]() x
x ![]() 5. Since the number of intervals
is not specified, Maple assumes four equal intervals by default:
5. Since the number of intervals
is not specified, Maple assumes four equal intervals by default:
>
simpson(x*sin(x^2),x=1..5);
![]()
> int(int(x^2*y^3,x=0..y),y=2..3);